Hey guys,
recently, I had to work on a project for my lecture on global illumination. My partner and I decided to implement a variant of the progressive photon mapping technique, described by Hachisuka et al.1 Instead of assigning each photon a certain color, we choose to map each photon to a certain wavelength which allowed us to simulate caustics more accurately and achieve effects splitting a beam of white light into its spectrum of colors:
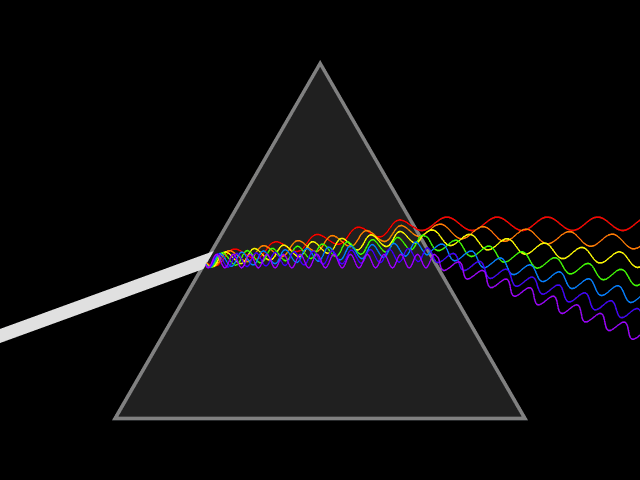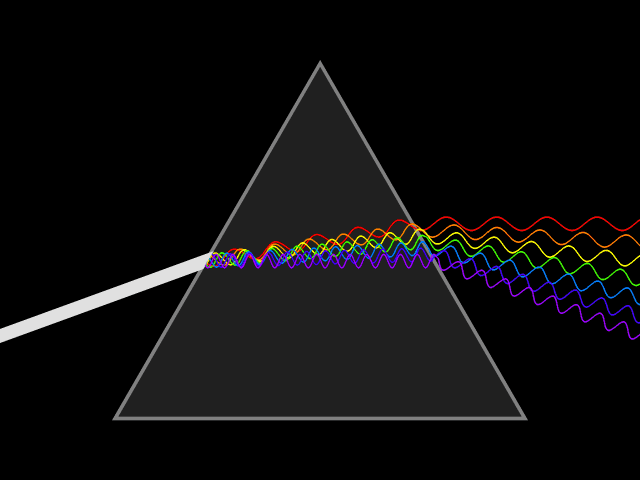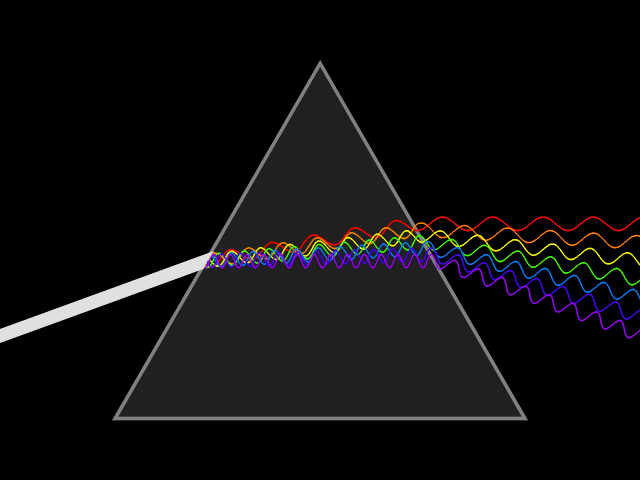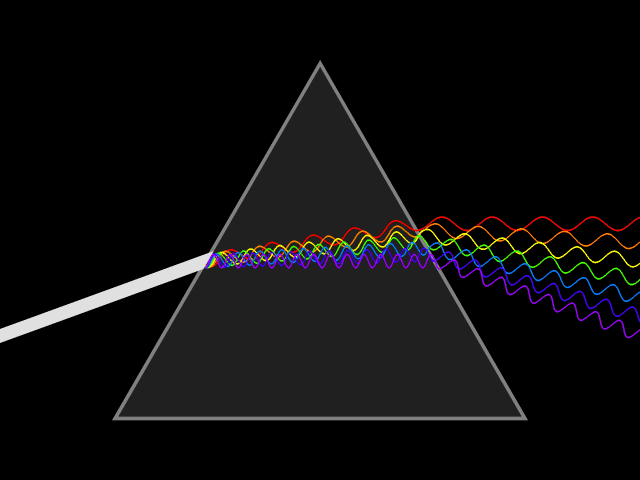
Dispersion of light
So instead of using the refraction index, that is often given for transparent materials, we used Cauchys equation2 to calculate the correct, individual refraction index for each photon:
$ n(\lambda) = B + \frac{C}{\lambda^2} $
Where lambda is the wavelength and B and C are material parameters, controlling the overall refraction and the variance depending on the wavelength. (Actually, the correct refraction index is given by the Sellmeier equation3, but for light in the visible spectrum the presented formula gives a reasonable approximation.)
There were a number of other problems we had to solve and I will probably create another post about this. So if you are interested in more technical details, let me know. But now, I want to show you some results.
The first scene is the standard cornell box with two spheres in it:
Cornell Box
The image on the left shows the noisy color-artifacts that are introduced with our method. This effect occurs, if the individual points in the scene did not receive enough photons, so that the average color is not the white, that is emitted from the light source. However, simply shooting more photons solves this problem and leads to the image on the right.
This looks pretty nice, but the interesting question was: does our implementation really produce the rainbow effect caused by a prism? So I created a scene with a narrow light source, which emits a beam of light at a prism and it turned out…

Rainbow Prism
…it does! :)